ASPL Manual v 1.00
© 2024 by SetSphere.COM
ASPL, A Set Programming Language, is a setadic calculator. The word setadic is introduced by the author to refer to a calculator whose symbolic operators are termed setadic operators and all of which perform algebraic set operations on datasets. These operators always precede their operands.
A setadic calculator, is a software appliance that takes structured data objects as input and breaks them into their constituent containment pathes so that they can be analyzed according to their structural components. ASPL maps algebraic data groups into containment pathes, and the appliance offers setadic operators to aggregate and to determine the relationships between their constituent elements. It renders them into a form suitable to be comprehended visually by the user before displaying their relationships on the user terminal.
Therefore, ASPL is an interactive software appliance that is started on the UNIX shell command prompt. Once ASPL is installed on the computer system, the user can start using it interactively to do sophisticated set operations, or can run ASPL scripts on the system where ASPL is installed. The ASPL interpreter provides a powerful and intuitive interactive computing facility that shares some similarities to a classic calculator. However, ASPL operators are set operators, and its variables are set variables. For the operator using ASPL, all variables are typeless and the commands are short and simple mnemonics that are easy to remember. ASPL does not require a database or any third party libraries. The program runs on UNIX systems where the standard Perl interpreter is available.
Your ASPL interpreter can perform a large number of sophisticated set operations using the preprogrammed set operators. The calculation results may then be assigned to variables called set variables. The set variables are presented as arguments to set operators to do further calculations. In addition, when you start the ASPL interpreter you are assigned a named workspace. It is this named workspace that is used by the ASPL instance to save the results and the variables of all your calculations. ASPL uses stacks to save the results performed by its operations, and uses internal symbol tables to save the variables. ASPL variables are all global variables, and when persistence is enabled these global variables are all shared by users connecting to the same workspace; in which case if two or more ASPL instances are started with the same named workspace then all variables are being shared globally by all ASPL instances. The workspace directory should be available to all instances.
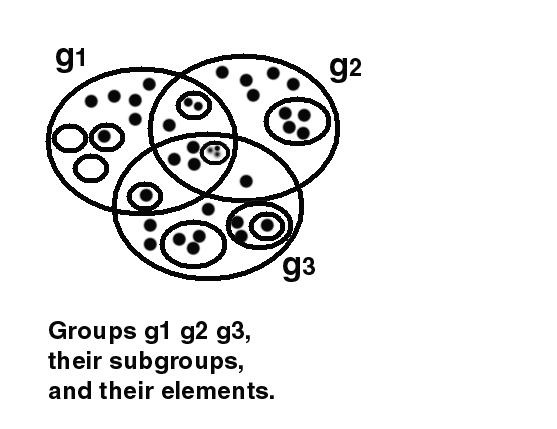
ASPL path containment can span multiple groups and subgroups along their elements. The following figure shows groups, subgroups, and their elements. There are three groups labeled g1, g2, and g3.
Note: ASPL groups image to be further explained in next Chapter using RANDONEBIT workspace
The labeled groups can be assigned to ASPL variables. For instance, v1, v2, and v3 are three ASPL variables that represent the groups g1, g2, and g3 respectively. ASPL setadic operators can then perform set operations on these variables. For instance to get the set union of all three groups: gU v1 v2 v3, to get their set intersection: g& v1 v2 v3, to get their set difference: g\ v1 v2 v3, and to get their set partitions: gP v1 v2 v3.
Notice the mnemonic of these four basic set operators: gU, g&, g\, and gP in which the first letter is a lower case 'g' depicting the subject on which the operation will take place, and the second letter (either one of U, &, \, and P) depicting the operation type. These four operators do the following operations, respectively:
Instruction Operation ----------- ------------------------- gU v1 v2 v3 get the group union considering the subrgoups and elements g& v1 v2 v3 get the group intersection considering the subrgoups and elements g\ v1 v2 v3 get the group difference considering the subrgoups and elements gP v1 v2 v3 partition the groups, subgroups, and their elementsIn a functional way these operations can also be further explained:
Instruction Operation ----------- ------------------------- gU v1 v2 v3 Union(v1, Union(v2,v3)) g& v1 v2 v3 Intersection(v1, Intersection(v1,v2)) g\ v1 v2 v3 Difference(v1, Difference(v2,v3) gP v1 v2 v3 Partition(v1,v2,v3)The subject denoted with the 'g' is to consider both the subgroups and elements in their respective groups. However, if the subject is only to do the operations on the subgroups then one can use dU, d&, d\ and dP. Therefore to get the set union of the subgroups only of all the three groups: dU v1 v2 v3, to get their set intersection: d& v1 v2 v3, to get their set difference: d\ v1 v2 v3, and to get their set partitions: dP v1 v2 v3.
One can look into the elements of the groups only (excluding the subgroups) by using fU, f&, f\ and fP. Therefore to get the set union of the elements only of all three groups: fU v1 v2 v3, to get their set intersection: f& v1 v2 v3, to get their set difference: f\ v1 v2 v3, and to get their set partitions: fP v1 v2 v3.
For ASPL this is done through its set builder for the setadic operation. For example, the intersection of the elements found in v1, v2, and v3, denoted with f& v1 v2 v3 is to parse (or humanly read) the information left to right: the set operator comes first (hence the meaning of setadic operator) then followed by the identifiers (representing the labeled groups or datasets). This is something that the reader is accustomed to from basic schooling, and can be seen through ASPL setbuilder by typing setbuilder f& v1 v2 v3 at the ASPL prompt:
aspl> setbuilder f& v1 v2 v3
QUOTIENT SET BUILDER
{f& v1 v2 v3} <=> f& v1 v2 v3
Detailed view:
{f& v1 v2 v3} <=>
f& v1 v2 v3
| | | +----> set-variable
| | +---------> set-variable
| +--------------> set-variable
+------------------> gets the elements intersection
Set builder syntax is read from left to right, or from bottom to top.
All ASPL setops are setadic: they take a setop followed by set variables.
To get the union of elements, one can type setbuilder gU v1 v2 v3 at the ASPL prompt:
aspl> setbuilder gU v1 v2 v3
QUOTIENT SET BUILDER
{gU v1 v2 v3} <=> gU v1 v2 v3
Detailed view:
{gU v1 v2 v3} <=>
gU v1 v2 v3
| | | +----> set-variable
| | +---------> set-variable
| +--------------> set-variable
+------------------> get the subgroups and the elements union
Set builder syntax is read from left to right, or from bottom to top.
All ASPL setops are setadic: they take a setop followed by set variables.
As for the intersection of subgroups and elements, one can type setbuilder g& v1 v2 v3 at the ASPL prompt:
aspl> setbuilder g& v1 v2 v3
QUOTIENT SET BUILDER
{g& v1 v2 v3} <=> g& v1 v2 v3
Detailed view:
{g& v1 v2 v3} <=>
g& v1 v2 v3
| | | +----> set-variable
| | +---------> set-variable
| +--------------> set-variable
+------------------> get the subgroups and the elements intersection
Set builder syntax is read from left to right, or from bottom to top.
All ASPL setops are setadic: they take a setop followed by set variables.
Each element within a group or subgroup can be further described and characterized by a set of attributes that are attached to it, and comparing it to another element is therefore based on these attributes. In ASPL every element has a checksum attribute, and the language provides a feature to subordinate setadic operators with a conditional predicate. Repeating the previous operation g& v1 v2 v3, but we want to get only these subgroups and elements that have different checksums, we will suffix the set operation g& with
`c~ as in setbuilder g&`c~ v1 v2 v3
aspl> setbuilder g&`c~ v1 v2 v3
QUOTIENT SET BUILDER
{g&`c~ v1 v2 v3} <=> g&`c~ v1 v2 v3
Detailed view:
{g&`c~ v1 v2 v3} <=>
g& ` c~ v1 v2 v3
| | | | | +----> set-variable
| | | | +---------> set-variable
| | | +--------------> set-variable
| | +------------------> have different checksums
| +---------------------> such that
+-----------------------> get the subgroups and the elements intersection
Here we used the acute backtick
` followed by a predicate. ASPL refers to this backtick simply with the word "tick" and
many of ASPL set operators can be ticked with specific predicates. For example, in the above example the operator is ticked with the predicate
saying "get the groups intersection of subgroups and elements when their checksums are differents" g&`c~.
In general, we are also accustomed to the forward slash, called the stroke or the solidus symbol /, that may follow a set operator to depict a quotient relation, and in ASPL this is called stroking a set operator. In the following example, the group intersection operator (g&) is being stroked with the quotient relation r3. Notice that the stroke is directly followed by a tilde then the relation r3. r3 has been defined by the user but expanded here as frx=.*$,mtm~ (that is saying to match the elements with regular expression .*$ and whose mtime attribute differ).
aspl> setbuilder g&/~r3 v1 v2 v3
QUOTIENT SET BUILDER
{g&/~r3 v1 v2 v3} <=> g&/frx=.*$,mtm~ v1 v2 v3
Detailed view:
{g&/~r3 v1 v2 v3} <=>
g& / frx=.*$,mtm~ v1 v2 v3
| | | | | | +----> set-variable
| | | | | +---------> set-variable
| | | | +--------------> set-variable
| | | +-------------------> have different make times
| | +--------------------------> file name regular expression
| +-------------------------------> stroking the Quotient Relation
+---------------------------------> get the subgroups and the elements intersection
The definition of r3 was performed with the command shown below and at any time the user can type q to display the quotient relation table:
aspl> q r3 := frx=.*$,mtm~
aspl> q
Coded QR
qr |user |code
------------------|--------------|------------------------------------
r3 |(1)root |frx=.*$,mtm~
This is equivalent to typing g&
`mtm~ v1 v2 v3 and in this particular case all the following three commands are equivalent:
aspl> g&/~r3 v1 v2 v3 aspl> g&/frx=.*$,mtm~ v1 v2 v3 aspl> g&`mtm~ v1 v2 v3
See appendix AAAAA on how to install ASPL on your UNIX system.
■ ASPL Building Blocks
Note: ASPL Startup TRIVIAL ASPLv1.00-startup-trivial.png
(* footnote: An interpreter typically has it own virtual machine, but ASPL does not. The ASPL interpreter is built on top of pure Perl interpreter and it uses the Perl powerful virtual machine in executing its tasks.)
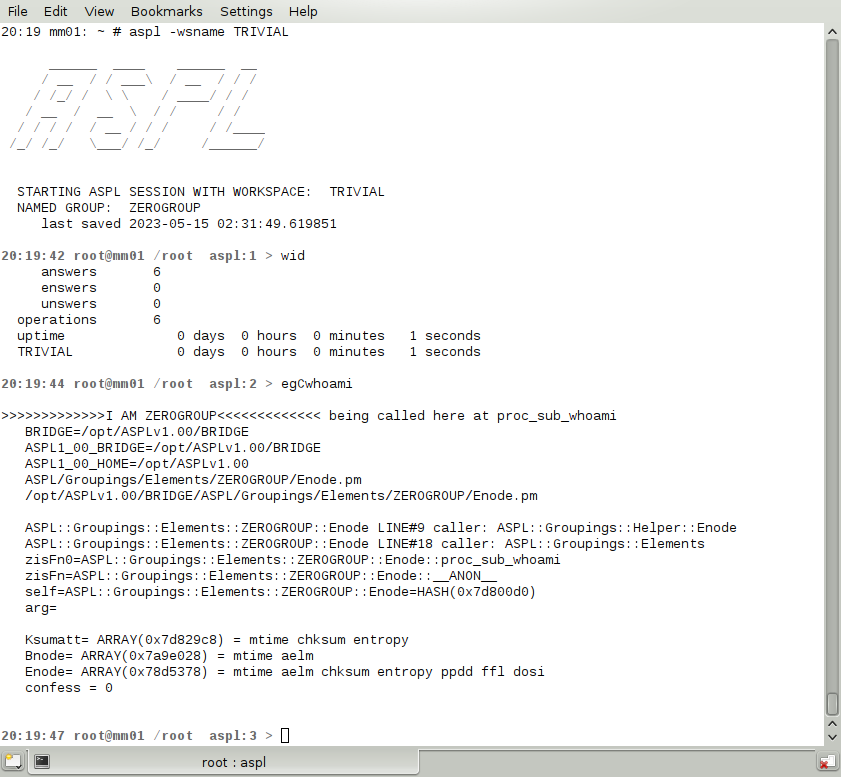
The TRIVIAL workspace is available with every ASPL distribution, and its grouping class is the ZEROGROUP which contains the bare information that is required by any grouping class in ASPL. The command wid displays the current workspace being loaded and its up time, and the command egCwhoami pings its grouping class container. Both commands are shown in Figure FFFFF.
Note: ASPL Startup TRIVIAL ASPLv1.00-startup-trivial.png
ASPL has eight major components:
- the syntax factory
- the set semantic processor
- the verbs transformer and dispatcher
- the set accumulator
- the set algorithmic processor
- the dynamically loadable container for the grouping classes
- the dynamically loadable container for generative functions
- the workspace manager for symbols and sessions management
These are shown in Figure FFFFF, and are also reflected in ASPL layout directories shown in Figure FFFFF.
Note: ASPL building blocks image ASPL-layout.png
[Top Text]
1. ASPLv1.00 2. |-- bin 3. |-- BRIDGE 4. | |-- ASPL 5. | | |-- BAYLEVELGROUP 6. | | | `-- Feeder 7. | | |-- EmStatv2 8. | | | `-- Cexec 9. | | |-- EmVectors 10. | | |-- Formattings 11. | | |-- GGs 12. | | | |-- GEO3TRI 13. | | | | `-- CTXSETOP 14. | | | |-- OSCILLATORSGROUP 15. | | | | `-- Feeder 16. | | | `-- SYSENVGROUP 17. | | | `-- Feeder 18. | | |-- Groupings 19. | | | |-- Elements 20. | | | | |-- ONEGROUP 21. | | | | `-- ZEROGROUP 22. | | | |-- Helper 23. | | | `-- stubs 24. | | `-- MockedGroupings 25. | | `-- MockedObjects 26. | `-- bin 27. |-- etc 28. |-- lib 29. | |-- ASPL 30. | | |-- ASPLSNTX 31. | | |-- Directory 32. | | | `-- DDM 33. | | |-- DISPLAY 34. | | |-- MemUsage 35. | | |-- PRIMITIVES 36. | | |-- SETACCUMULATOR 37. | | |-- SOPALGO 38. | | |-- SOPVERBS 39. | | |-- SOPX 40. | | |-- SYMBOPS 41. | | | `-- FTX_VERBPROCESSORS_BUILDER 42. | | `-- Utilities 43. | `-- Simple 44. |-- license 45. `-- shared 46.
[Top Text]
1. ASPLv1.00 2. |-- bin 3. |-- BRIDGE 4. | |-- ASPL 5. | | |-- BAYLEVELGROUP 6. | | | `-- Feeder 7. | | |-- EmStatv2 8. | | | `-- Cexec 9. | | |-- EmVectors 10. | | |-- Formattings 11. | | |-- GGs 12. | | | |-- GEO3TRI 13. | | | | `-- CTXSETOP 14. | | | |-- OSCILLATORSGROUP 15. | | | | `-- Feeder 16. | | | `-- SYSENVGROUP 17. | | | `-- Feeder 18. | | |-- Groupings 19. | | | |-- Elements 20. | | | | |-- ONEGROUP 21. | | | | `-- ZEROGROUP 22. | | | |-- Helper 23. | | | `-- stubs 24. | | `-- MockedGroupings 25. | | `-- MockedObjects 26. | `-- bin 27. |-- etc 28. |-- lib 29. | |-- ASPL 30. | | |-- ASPLSNTX 31. | | |-- Directory 32. | | | `-- DDM 33. | | |-- DISPLAY 34. | | |-- MemUsage 35. | | |-- PRIMITIVES 36. | | |-- SETACCUMULATOR 37. | | |-- SOPALGO 38. | | |-- SOPVERBS 39. | | |-- SOPX 40. | | |-- SYMBOPS 41. | | | `-- FTX_VERBPROCESSORS_BUILDER 42. | | `-- Utilities 43. | `-- Simple 44. |-- license 45. `-- shared 46.
Starting ASPL in verbose mode will also reflect where ASPL loads its components at startup as shown in Figure FFFFF.
ASPL Startup on the UNIX Shell Prompt Explained
A user interacting with ASPL places a setadic operation to the interpreter. The interpreter submits it to the syntax factory, analyzes it, builds its object, and locates its verb. It then dispatches the object to its algorithmic set processing agent after fetching its symbols from either the answer stack or the symbol table. The result of the processed expression is finally saved in the symbol table, pushed on the top of the stack, and displayed on the terminal. The simplest way to see the flow of ASPL processing is to enable the tracing facility of ASPL (see Appendix CCCCC).
■ ASPL Commands with asplcmd
At this point we introduce the asplcmd command because it is a quick way to execute short ASPL statements through the UNIX shell prompt.
You can direct ASPL to execute some of its statements by issuing asplcmd at the shell prompt followed by a a string. If the string is more than a word then it must be quoted since it is passed like a single argument to asplcmd. Without going into details on how asplcmd works, as this will become clear after reading the chapter "ASPL Scripts", it is used here to facilitate some explanation on ASPL displayable output.
The following command compares the datasets saved in the variable mg123 of workspace RANDONEBITMIX.
# asplcmd 'load RANDONEBITMIX;gU mg123'
The following command compares two variables a2 and a7 that has been saved in workspace WS1.
# asplcmd 'load WS1; ks mtime chksum ppdd; gU a2 a7'
When you pass a string to asplcmd the interpreter will parse the string and execute its contents then exit.
■ ASPL Symbolic Shemes and Colors
ASPL is not a GUI application and does not require any GUI API, it uses plain ASCII characters for its symbolic operators and identifiers, and uses the ANSI colors scheme provided by the UNIX terminal. (* footnote: APL users should be alarmed as there is no APL Greek symbols in here!) At any time you can start ASPL at the UNIX shell prompt of a terminal (or even on a dumb terminal) or an X Window session. Figure FFFFF-1 shows ASPL started in a KDE session.
Because the set comparison operators classify data into three basic categories: intersection, union, and difference, then it is recommended to display the output using three different colors. In addition, since a group may contain subgroups and elements, then some symbolic scheme is needed to show the group differences along these colors. ASPL uses both colors and symbolic schemes to facilitate the readability of its output. Using the ANSI colors that is readily available on all UNIX terminal, and compounding it with symbolic schemes will help to distinguish when subgroups and elements are unique, equal, or different.
Figure FFFF shows the partial result of the command discussed in the previous section:
# asplcmd 'load RANDONEBITMIX;gU mg123'
To understand the meaning of ASPL colors and symbolic schemes let's go over figure FFFF where the output has been labeled at five points as follow:
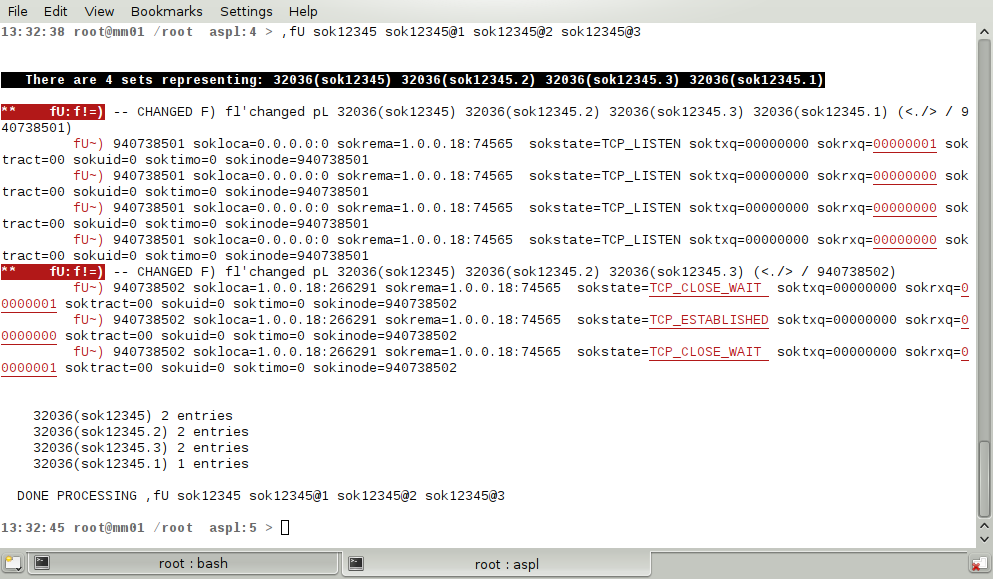
① gU: f!=) this is the gU of g1 g2 g3 where a difference in the element has been detected: it is the subgroup df2 that was detected in the subgroup ./df2/df1
② gU: +f) element df3 only in subgroup ./df2/df1/ in group g3
③ gU: d!=) subgroup df2 in subgroup ./df2/ in all groups g1 g2 and g3 but they differ
④ gU: f==) element df1 in subgroup ./df2/df2/ in all groups g1 g2 and g3 and is the same
⑤ gU: g!=) mixed as df3 is ./df2/ is subgroup in groups g1 g2 and it is an element in group g3
Note: ASPL Symbolic Shemes and Colors g1g2g3-12345.png
This example might be confusing, but it was selected on purporse to make it clear that the label names of subgroups and elements are immaterial to ASPL algorithmic routines.
Let's take a look at another practical example where a file name and a directory name might intersect on the UNIX filesystem. Assuming you have access to the /tmp directory, issue the following commands on your shell prompt:
# mkdir /tmp/foodir1
# mkdir /tmp/foodir1/abc
# mkdir /tmp/foodir2
# touch /tmp/foodir2/abc
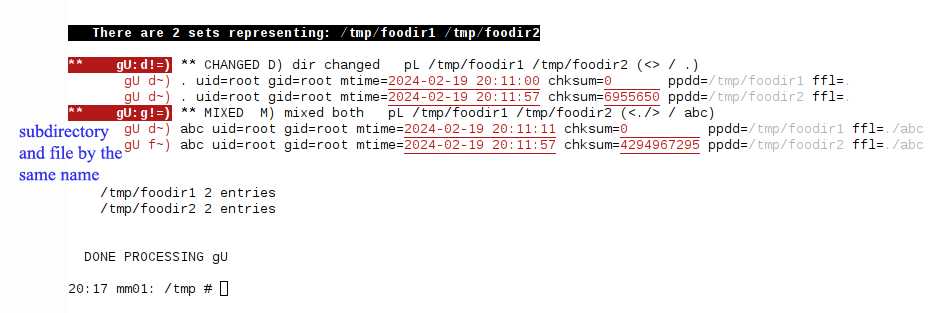
# asplcmd "createworkspace TRANSIENT POSIX;ggdir(dir,/tmp/foodir1);ggdir(dir,/tmp/foodir2);gU"
The first two commands create a directory and a subdirectory /tmp/foodir1 and /tmp/foodir1/abc respectively, and the next two commands create a directory and a file /tmp/foodir2 and /tmp/foodir2/abc respectively. The last command call ASPL to show the difference between the two directories /tmp/foodir1 and /tmp/foodir2.
The statement createworkspace TRANSIENT POSIX tells ASPL to load the temporary TRANSIENT workspace with element grouping class POSIX. The next statement ggdir(dir,/tmp/foodir1) tells ASPL to call the grouping function ggdir() on directory /tmp/foodir1. These statements will become clearer in the next chapters. For now, if you have issued these command succeffully then you are already using ASPL.
The result of comparing the comparing the directories is shown below: Note: Example comparing a file and a subdirectory that have the same name foodir-commented.png
Appendix DDDD shows a summary of ASPL symbolic schemes and how the user can edit the color configuration settings.
■ Why do you need to use ASPL
There are myriad reasons why you need to use the ASPL interpreter: to detect and highlight changes of systemic data in a UNIX cloud environment, to validate configuration data in a UNIX cluster, to resolve collision of class names in JAR archives, to compare analogous PATH across systems, etc. The following figure shows the result of a UNIX system whose socket has changed states:
Figure monitor-socket-state.png
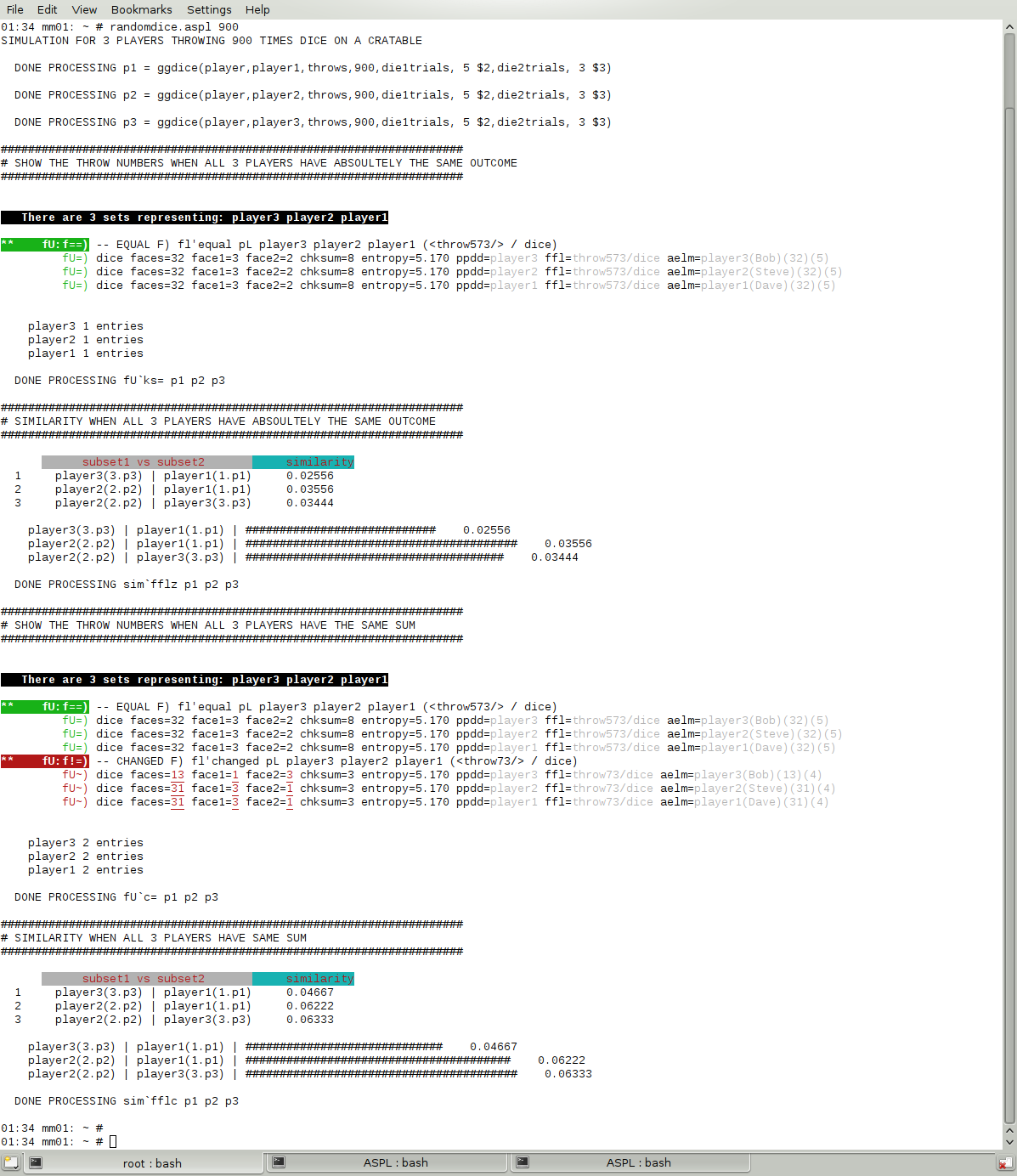
Furthermore one can use ASPL to do simulation of players throwing dice on a crap table. Figure FFFFF shows the result of the simulation of players tossing dice: find the event when all the three players have the same outcome.
Figure randomdice.aspl-900.png
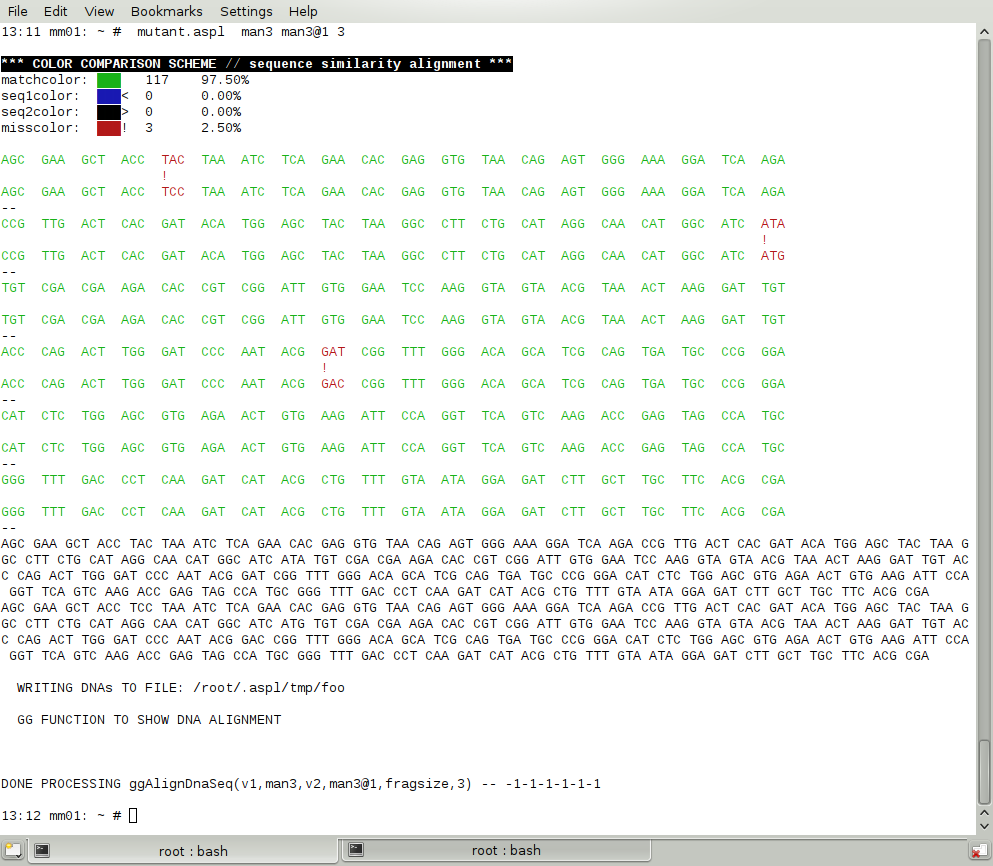
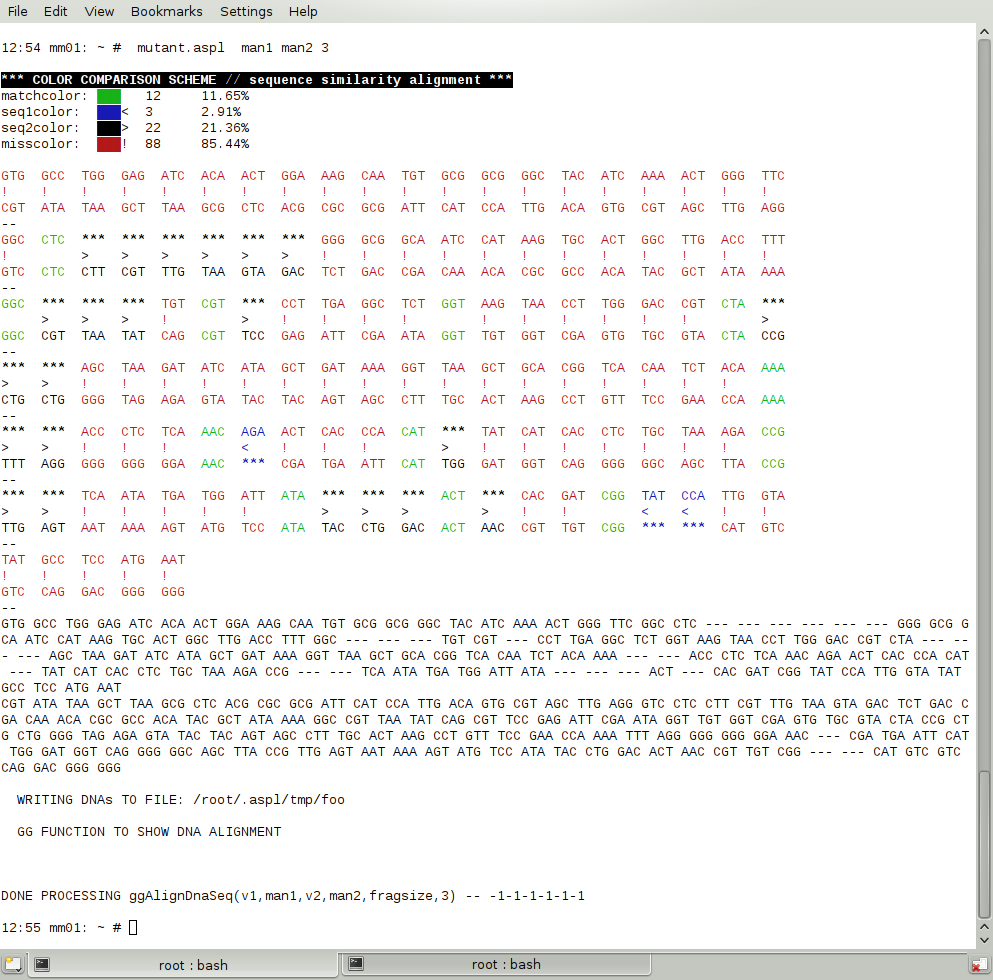
ASPL can also treats DNA sequences as datasets and you can toy with these sequences through its alignment algorithms. Figure FFFFF shows a mutant when altering the sequence randomly, and figure FFFFF show the DNA sequence alignment of two men.
Figure mutant.aspl-img1.png
Figure mutant.aspl-img.png
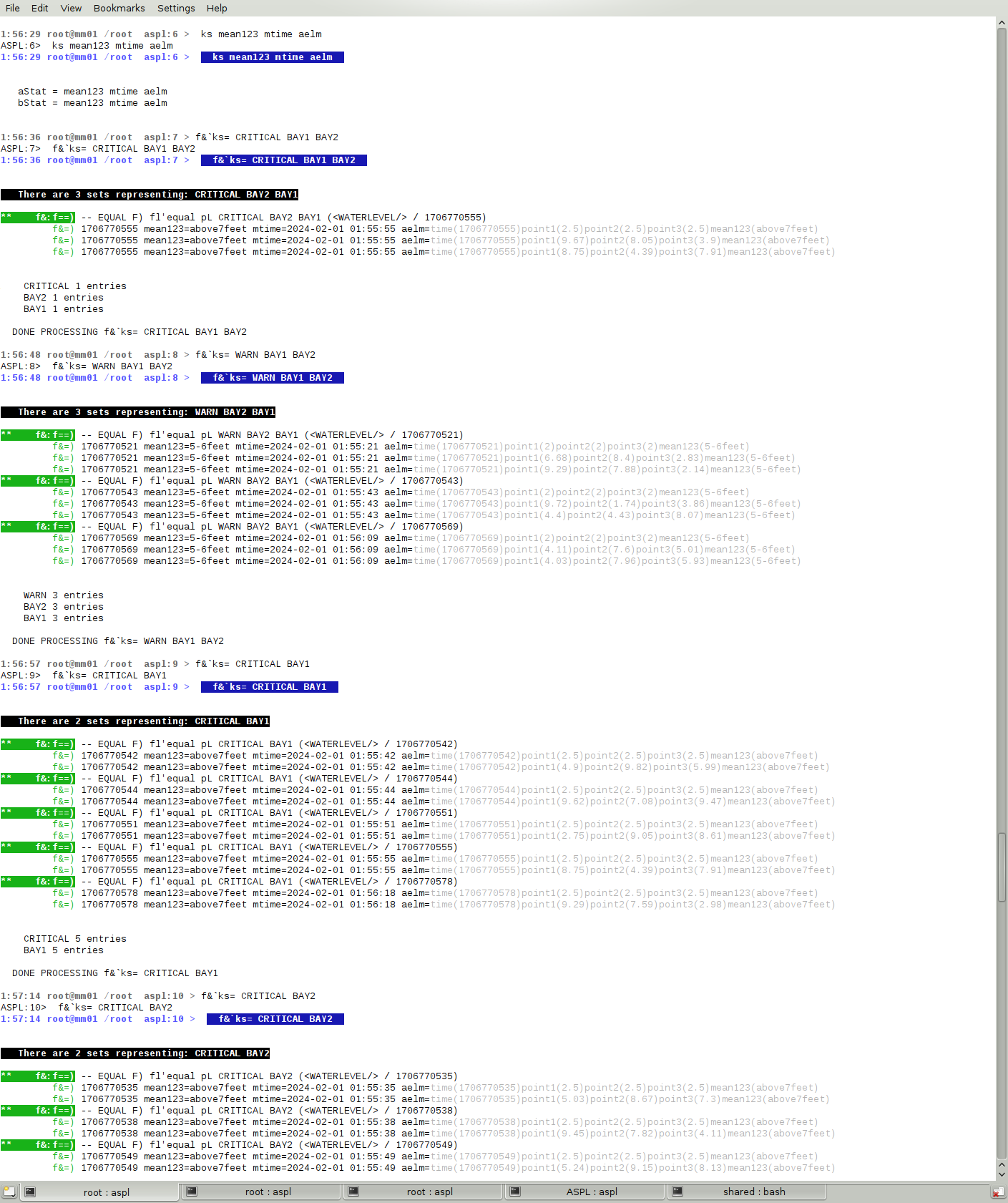
The elements of a group do not need to be the usual static data, as an element attributes can be renewed when hooked to processes or tied to devices in a system that may change states. We will see some examples in "ASPL by Examples" where the OSCILLATORGROUP defines attributes that are tied to a device to collect data set; and another example using the BAYLEVELGROUP whose attributes are tied to sensors monitoring the water level between two bays. Figure FFFFF shows a simulation when the water level between the two bays is critical.
BAYS12MON-img0.png
ASPL can do fuzzy set operations, these are simple operators like y&, yU, and y\ to get the fuzzy intersection, union, and difference respectively.
With its powerful regular expression processor, ASPL can do shallow set operations. Just type shallowed and you select the shallow matching that you desire.
A quick view of the shallow table module is shown below.
aspl:1 > shallowed
THE SHALLOW MATCHING IDENTIFIER TO SELECT THE ROUTINE WHEN SHALLOW SETOPS ARE USED:
IDENTIFIER DESCRIPTION
---------- -----------
nothing matching nothing at all
starstar matching anything and everything
matchandmatch matching the ./subgroups and the element
matchormatch matching the ./subgroups or the element
elem matching just the element and ignoring ./subgroups
stem matching just the ./subgroups and ignoring the element
endjoinedeither matching from end of ./subgroups/element for either
begjoinedeither matching the beginning of ./subgroups/element for either
endstem matching just the ./subgroups from the end and ignoring the element
endstemeither matching just the ./subgroups from the end and ignoring the element (for either)
begstem matching from beginning of ./subgroups while ignoring the element
begstemeither matching from beginning of ./subgroups while ignoring the element (for either)
piecedstem matching at least one piece in ./subgroups while ignoring the element
> piecedstemelem matching the element and at least one piece in the ./subgroups
begelem matching from the beginning of element and ignoring ./subgroups (for either)
endelem matching from the end of element and ignoring ./subgroups (for either)
rgxelem matching the element anywhere and ignoring ./subgroups (for either)
prcrelem apply processor when matching the element anywhere and ignoring ./subgroups (for either)
CURRENTLY LOADED piecedstemelem
WHEN SELECTING prcrelem AS THE SHALLOW MATCHING IDENTIFIER, ONE OF THE FOLLOWING
NODE PROCESSOR IDENTIFIER CAN BE SELECTED:
IDENTIFIER EVAL DESCRIPTION
---------- ---- -----------
transac 1 capture the element where word Transaction occured, ignore case
cla2ja 1 substitute .class with .java
ja2cla 1 substitute .java with .class
uc 1 upper case
lc 1 lower case
> asis 1 neutral without any change
CURRENTLY LOADED PROCESSOR asis
THE shallowedMatches PACKAGE CAN BE EDITED TO ADD MORE MATCHING SUBROUTINES.
SEE ASPL CONFIGURATION FILES FOR MORE ABOUT EDITING shallowedMatches PACKAGE.
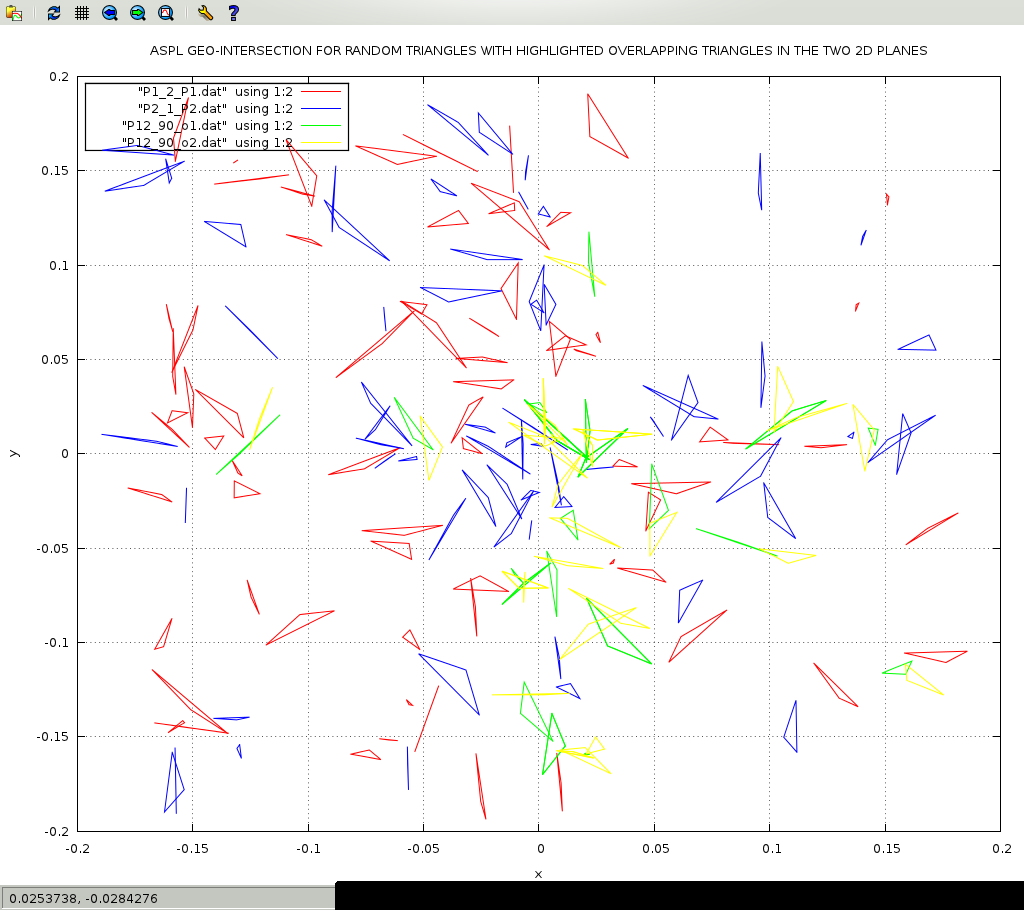
Moreover ASPL can switch its set operation mode to do geometric set operations so that you can detect intersecting polygons in 2D planes or on spheres.
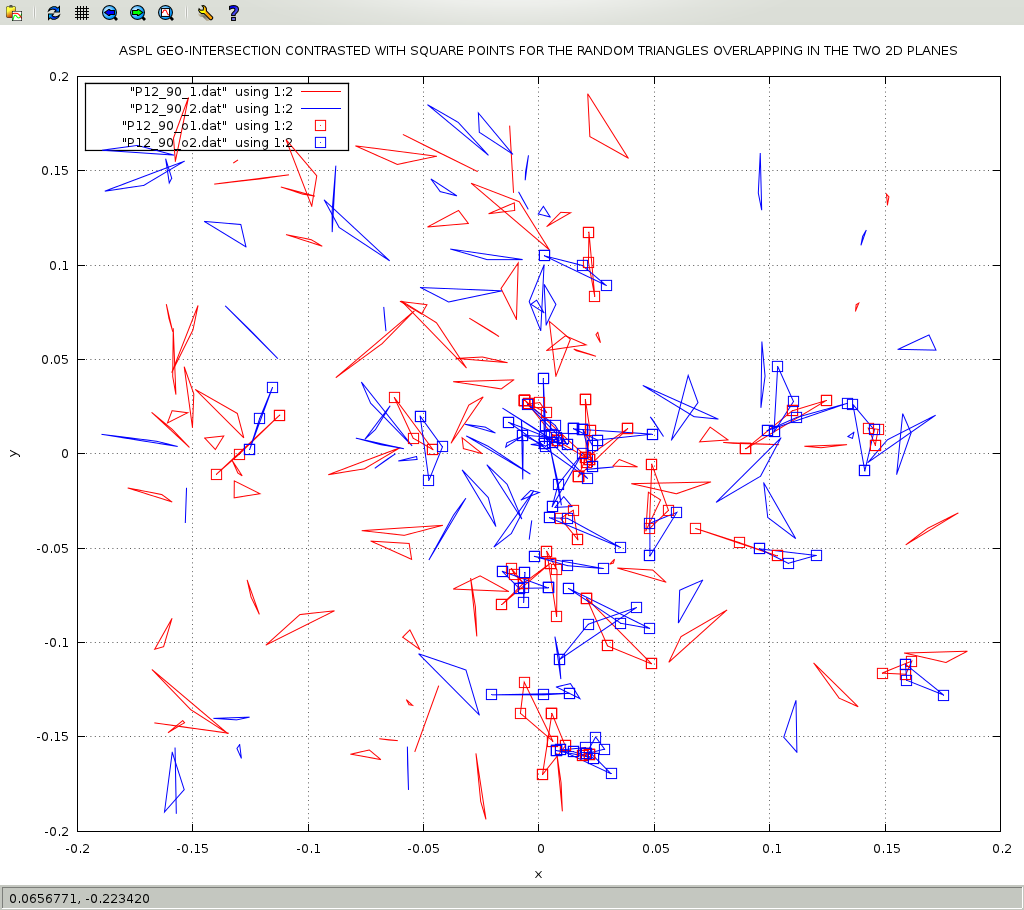
Figure FFFFF shows the intersecting polygons in two planes. The intersecting polygons are contrasted by showing their vertex in squares.
P12_90-both-and-intersect-img2.png
Figure P12_90-both-and-intersect-img2.png
P12_90-both-and-intersect-img1.png
PUBLISHER VERSION USING SQUARE POINTS FOR BLACK AND WHITE PRINT
Figure P12_90-both-and-intersect-img1.png
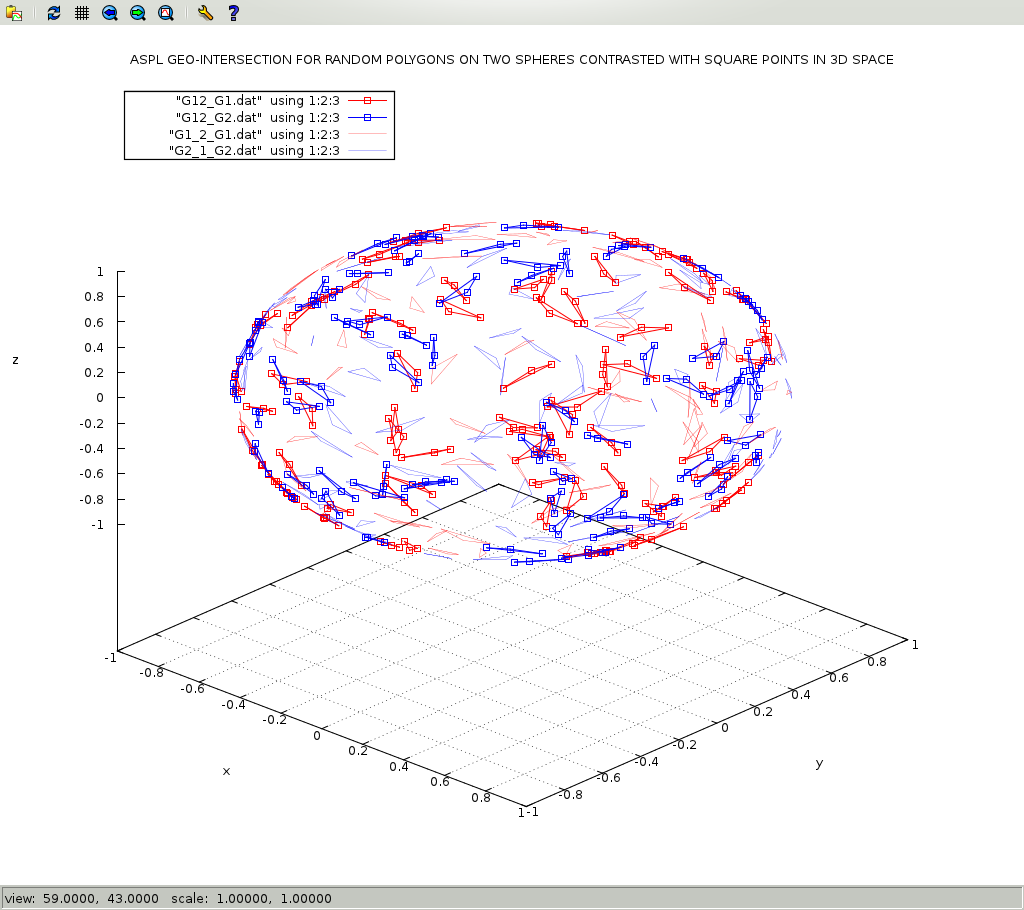
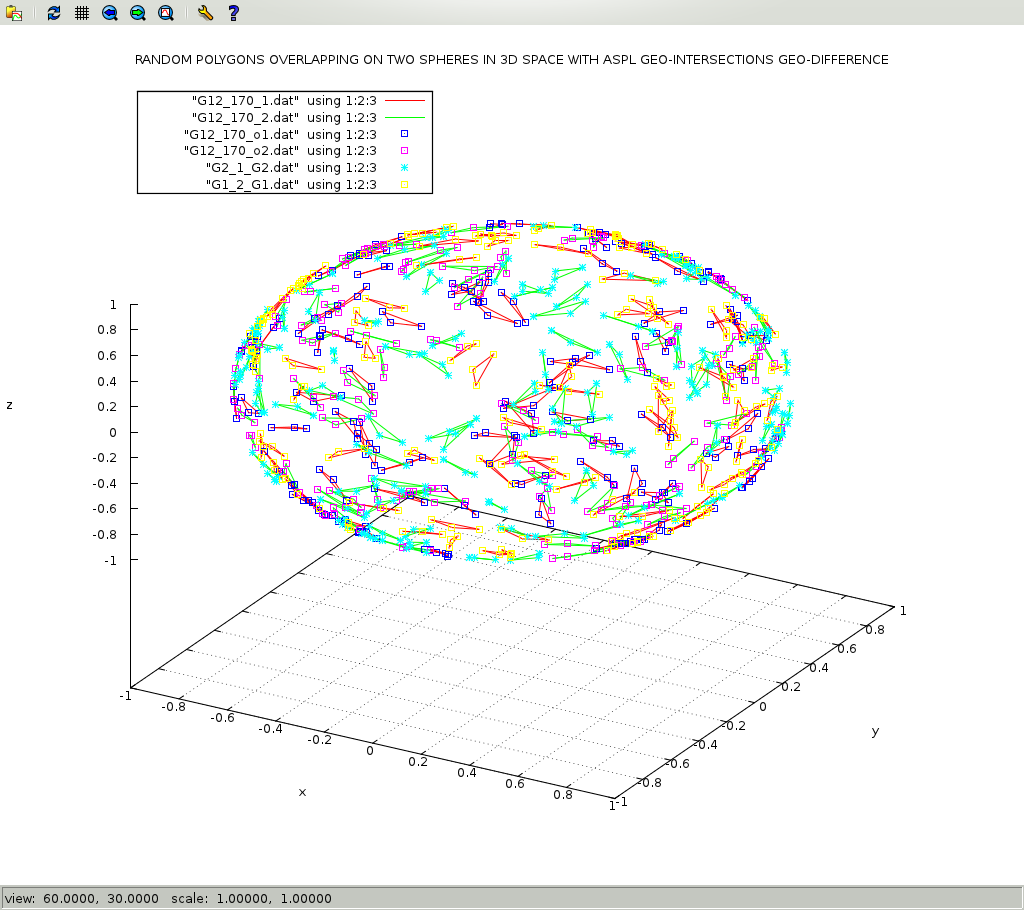
Figure FFFFF shows the intersecting polygons on two spheres, and figure FFFF shows the intersects and differences between these polygons.
G12_170-all-with-intersect-img3D.png
Figure G12_170-all-with-intersect-img3D.png
Refer to see SECTION 11.14.1 [RANDOM POLYGONS ON THREE SPHERES]
G12_170-both-all-img3D.png
Figure G12_170-both-all-img3D.png
Many of these examples are detailed in see SECTION 11.1.1 [ASPL by Examples]
Chapter Ref:ASPL by Examples
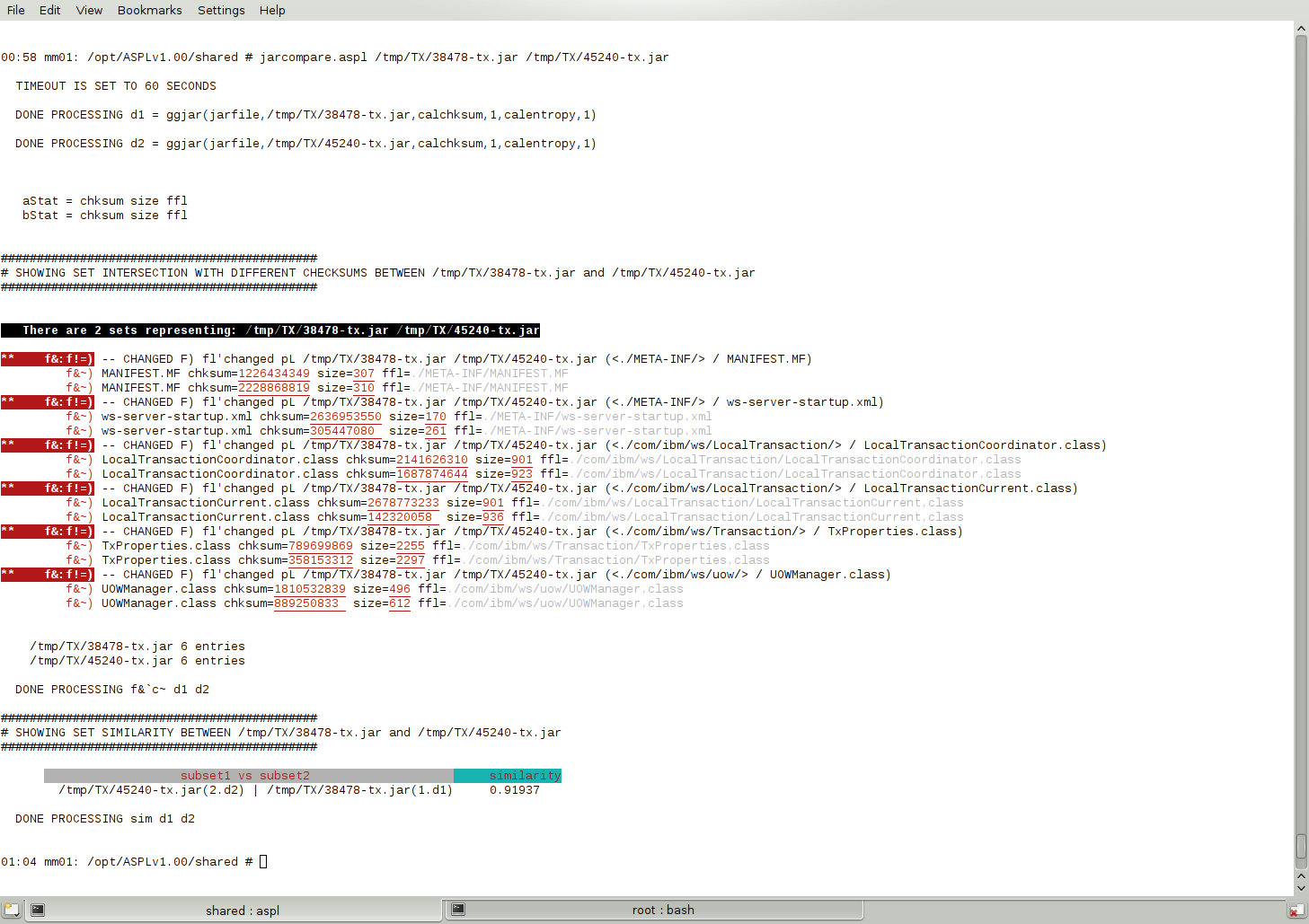
In addition the interpreter offers the ASPL scripting language so that you can enhance your system with powerful commands. Consider the following script that displays the differences between JAR archives. It can be run on the UNIX prompt with the simple command jarcompare.aspl jarfile1 jarfile2.
[Top Text]
LISTING jarcompare.aspl ASPL Script jarcompare.aspl1. #!/usr/bin/env aspl 2. #ENVARG= -groupingclass POSIX -wsname TRANSIENT -singlepass 3. 4. ;;*********************************************************************** 5. ;; jarcompare.aspl 6. ;; Compare two JAR archives 7. ;; Copyright © 2024 Bassem W. Jamaleddine 8. ;; 9. ;;*********************************************************************** 10. 11. endScriptIfShellArgsLessThan 2 12. 13. timeout 60 14. displayoff 15. d1 = ggjar(jarfile,$1,calchksum,1,calentropy,1) 16. d2 = ggjar(jarfile,$2,calchksum,1,calentropy,1) 17. 18. displayon 19. ks chksum size ffl 20. print ############################################ 21. print # SHOWING SET INTERSECTION WITH DIFFERENT CHECKSUMS BETWEEN $1 and $2 22. print ############################################ 23. f&`c~ d1 d2 24. print ############################################ 25. print # SHOWING SET SIMILARITY BETWEEN $1 and $2 26. print ############################################ 27. sim d1 d2 28. println 29. 30. endscript 31. 32. __END__ 33. 34. $00 compares two JAR archives 35. 36. $00 must be followed by the names of two JAR archives 37. 38. Example: To compare the two JAR archives /tmp/TX/27238-tx.jar and /tmp/TX/38141-tx.jar 39. 40. $00 /tmp/TX/27238-tx.jar /tmp/TX/38141-tx.jar 41.
Figure FFFFF shows the result of jarcompare.aspl when comparing two JAR achives. Notice how the colliding names of the classes have been detected and their different checksums is displayed in red color.
Figure jarcompare.aspl-img.png
Another variation of the jarcompare.aspl script where the DEF FN defines the function "cmp2sets" for extended groups comparison is shown below:
[Top Text]
LISTING jarcompare2.aspl ASPL Script jarcompare2.aspl1. #!/usr/bin/env aspl 2. #ENVARG= -groupingclass POSIX -wsname TRANSIENT -singlepass 3. 4. ;;*********************************************************************** 5. ;; jarcompare.aspl 6. ;; Compare two JAR archives 7. ;; Copyright © 2024 Bassem W. Jamaleddine 8. ;; 9. ;;*********************************************************************** 10. 11. endScriptIfShellArgsLessThan 2 12. 13. DEF FN cmp2sets := {gU {g\, %%1 %%2}{g\, %%2 %%1}{g&, %%1 %%2}} 14. 15. timeout 60 16. displayoff 17. d1 = ggjar(jarfile,$1,calchksum,1,calentropy,1) 18. d2 = ggjar(jarfile,$2,calchksum,1,calentropy,1) 19. 20. displayon 21. ks chksum size mtime ffl 22. print ############################################ 23. print # SHOWING SET COMPARISONS BETWEEN $1 and $2 24. print ############################################ 25. FN cmp2sets(d1,d2) 26. print ############################################ 27. print # SHOWING SET INTERSECTION WITH DIFFERENT CHECKSUMS BETWEEN $1 and $2 28. print ############################################ 29. f&`c~ d1 d2 30. print ############################################ 31. print # SHOWING SET SIMILARITY BETWEEN $1 and $2 32. print ############################################ 33. sim d1 d2 34. println 35. 36. endscript 37. 38. __END__ 39. 40. $00 compares two JAR archives 41. 42. $00 must be followed by the names of two JAR archives 43. 44. Example: To compare the two JAR archives /tmp/TX/27238-tx.jar and /tmp/TX/38141-tx.jar 45. 46. $00 /tmp/TX/27238-tx.jar /tmp/TX/38141-tx.jar 47.
Naturally the ASPL interpreter allows you to do set operation interactively at its prompt and the user can repeat the same operations shown in the script at the ASPL prompt. Writing scripts with ASPL is simple as you will see in Chapter "ASPL Scripts".
ASPL uses the notion of grouping class and treats algebraic groups per their meta data. The grouping class specially characterizes the set of data being treated.
ASPL Elements Class Containment is discussed in Chapter "ASPL A DETAILED VIEW".
ASPL is premier set calculator uniquely identified with its powerful programming of set elements and their attributes: ASPL element attributes can be statically defined, or dynamically updatable by anonymous subroutines, or refreshable with new data when tied to generative devices. When a change is detected in an element, ASPL archives the variable, and you can use set operators to display what has changed.