ASPL Guide to Operations v 1.00
© 2024 by SetSphere.COM


4. 13
   gU gets the subgroups and the elements union

 

logo

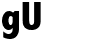
gU a1 [a2 .. aN]       where a1 [a2 .. aN] are set variables

gU`mtm~ a1 [a2 .. aN]

gU/mtm~ a1 [a2 .. aN]

gU

When specified by itself then the operation is performed on the object on top of the stack and the one that is one below it, then the result is pushed on the stack

setop  setoid  1**  commu        ins:H_H_H  ous:H_H_H

●  Operator gU gets the subgroups and the elements union

Use the operator gU to get the groups union of one or many datasets. This set operator can be followed by one or many set variables, and the set union is for the elements based on the group label or labels defined in the set variables. If the same named label is used in different set variables then you can labinate the set operation using ,gU or gU,.
See also how to get the elements union see SECTION 4.3.1 [fU gets the elements union] .

 

gU EXAMPLE1
The following example shows how to find the union of subdirectories and files found in three different directories of WS1 datasets. We start ASPL by loading the sample workspace WS1 and issue the operation gU on the set variables.

 

gU OPERATION1

# aspl WS1
    (start ASPL loading the sample workspace WS1)

①  aspl> gU a1 a2 a3
    (get groups union of a1 a2 a3)

②  aspl> a123 = gU a1 a2 a3
    (assign a123 to the groups union of a1 a2 a3)

③  aspl> v
    (view symbol table)

④  aspl> display a123
    (display the set variable a123)

 

gU EXAMPLE2
The following example shows how to find the union of subdirectories and files found in a directory and its archive. We start ASPL by loading the sample workspace WS1, we interrogate the set variable a1, then issue the labinated operation ,gU on the set variables.

 

gU OPERATION2

# aspl WS1
    (start ASPL loading the sample workspace WS1)

①  aspl> v sorted
    (display the symbol table showing the archived variables)

②  aspl> ? a1
    (interrogate the a1 set variable updating it)

③  aspl> v sorted
    (display the symbol table showing the archived variables)

④  aspl> ,gU a1 a1@1
    (get groups union of a1 and its archived a1@1)

 

● Tickable Predicates for gU

This gU is tickable with predicates that are shown in the following table:

       a yellow note
gU`_  gets the subgroups and the elements union 
gU`c=  gets the subgroups and the elements union such that they have the same checksum 
gU`c~  gets the subgroups and the elements union such that they have different checksums 
gU`c~~  gets the subgroups and the elements union such that they have all over different checksums 
gU`h=  gets the subgroups and the elements union such that they have the same entropy 
gU`h~  gets the subgroups and the elements union such that they have different entropies 
gU`h~~  gets the subgroups and the elements union such that they have all over different entropies 
gU`mtm=  gets the subgroups and the elements union such that they have the same make time 
gU`mtm~  gets the subgroups and the elements union such that they have different make times 
gU`mtm~~  gets the subgroups and the elements union such that they have all over different make times 
gU`ks=  gets the subgroups and the elements union such that they have the same ksum 
gU`ks~  gets the subgroups and the elements union such that they have different ksums 
gU`ks~~  gets the subgroups and the elements union such that they have all over different ksums 
(C)2024 ASPL Inc.