ASPL Manual v 1.00
© 2024 by SetSphere.COM


13. 5
   disjoint determines if two sets are disjoint

 

logo

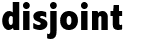
disjoint a1 a2 .. aN       where a1 a2 .. aN are set variables

disjoint a1 a2

disjoint  context  2  commu        ins:H_H_H  ret:context

●  disjoint determines if two sets are disjoint

Use this disjoint to determine if two datasets are disjoint. Two datasets are disjoint if and only if they have no common named elements or named subgroups. You can also follow the disjoint operator by two or more set variables, in which case the operator return true if all the set variables are disjoint.

 

disjoint EXAMPLE1

In the following example we will get the symmetric difference of the elements between two datasets a1 and a2.

We will compare it to the intersection of their elements, which obviously must be disjoint.

 

disjoint OPERATION1

# aspl WS1

①  aspl> fu12 = fU a1 a2
    (get the elements union in fu12)

②  aspl> fi12 = f& a1 a2
    (get the elements intersection in fi12)

③  aspl> disjoint fi12 fu12
    (these are not disjoint)

④  aspl> mostlydisjoint fi12 fu12
    (this will be true yet depend on mostly amplifier)

⑤  aspl> df12 = f\ fu12 fi12
    (get the difference of elements between the union and the intersection, set it in df12)

⑥  aspl> Df12 = fD a1 a2
    (or simply get the symmetric difference with fD, set in in Df12)

⑦  aspl> equal df12 Df12
    (these must be equal)

⑧  aspl> disjoint df12 fi12
    (and these must be disjoint)

⑨  aspl> disjoint Df12 fi12
    (and so these must be disjoint)

⑩  aspl> disjoint Df12 fi12 a1
    (test disjoint with three set variables)

⑪  aspl> disjoint Df12 fi12 a3
    (test disjoint with three set variables)

⑫  aspl> disjoint a1 a2 a3 a4
    (test disjoint with four set variables)

 

disjoint EXAMPLE2

The g's operators, like gU, do the operations on groups, subgroups, and elements. A labeled subgroup that has the same name as an element within a group (or subgroup) will be captured by g's operators. The following operations show such an example.

 

disjoint OPERATION2

# aspl WS1

①  aspl> disjoint a1 a2

②  aspl> gu12 = gU a1 a2
    (pay attention to ./WSADMIN/OPOP )

pay attention to ./WSADMIN/OPOP which is a subgroup name in one group and an element name in the other group. This will break the dijointness below

③  aspl> gi12 = g& a1 a2

④  aspl> disjoint gi12 gu12

⑤  aspl> dg12 = g\ gu12 gi12

⑥  aspl> Dg12 = gD a1 a2

⑦  aspl> equal dg12 Dg12

⑧  aspl> disjoint dg12 gi12
    (these are not disjoint because of gu12 )

⑨  aspl> disjoint Dg12 gi12
    (these are not disjoint because of gu12 )

 

● DISJOINTNESS and its Amplifiers

This disjoint can be amplified by prefixing it with amplification syntax shown in the following table:

       a yellow note
Disjoint  determines if two or more sets are disjoint 
mostlyDisjoint  determines if two or more sets are mostly disjoint 
looselyDisjoint  determines if two or more sets are loosely disjoint 
mostlyLooselyDisjoint  determines if two or more sets are mostly loosely disjoint 
noeattrDisjoint  determines if two or more sets (ignoring the attributes) are disjoint 
mostlyNoeattrDisjoint  determines if two or more sets (ignoring the attributes) are mostly disjoint 
looselyNoeattrDisjoint  determines if two or more sets (ignoring the attributes) are loosely disjoint 
mostlyLooselyNoeattrDisjoint  determines if two or more sets (ignoring the attributes) are mostly loosely disjoint 
(C)2024 ASPL Inc.